What Two Measurable Properties Directly Tell Us The Size And Shape Of A Planet's Orbit?

Curved path of an object effectually a point

Two bodies of dissimilar masses orbiting a common barycenter. The relative sizes and type of orbit are like to the Pluto–Charon system.

In angelic mechanics, an orbit is the curved trajectory of an object^[1] such equally the trajectory of a planet around a star, or of a natural satellite around a planet, or of an artificial satellite around an object or position in space such as a planet, moon, asteroid, or Lagrange bespeak. Normally, orbit refers to a regularly repeating trajectory, although it may also refer to a not-repeating trajectory. To a close approximation, planets and satellites follow elliptic orbits, with the center of mass being orbited at a focal betoken of the ellipse,^[2] as described by Kepler'due south laws of planetary motion.

For near situations, orbital motion is adequately approximated by Newtonian mechanics, which explains gravity as a force obeying an changed-foursquare law.^[3] Nevertheless, Albert Einstein's general theory of relativity, which accounts for gravity as due to curvature of spacetime, with orbits following geodesics, provides a more accurate calculation and agreement of the verbal mechanics of orbital move.

History [edit]

Historically, the apparent motions of the planets were described by European and Arabic philosophers using the idea of angelic spheres. This model posited the existence of perfect moving spheres or rings to which the stars and planets were fastened. It assumed the heavens were fixed autonomously from the motion of the spheres and was developed without any agreement of gravity. After the planets' motions were more accurately measured, theoretical mechanisms such as deferent and epicycles were added. Although the model was capable of reasonably accurately predicting the planets' positions in the heaven, more and more than epicycles were required equally the measurements became more accurate, hence the model became increasingly unwieldy. Originally geocentric, it was modified by Copernicus to identify the Sun at the center to aid simplify the model. The model was further challenged during the 16th century, as comets were observed traversing the spheres.^[iv] ^[v]

The basis for the modern agreement of orbits was kickoff formulated by Johannes Kepler whose results are summarised in his three laws of planetary motion. First, he found that the orbits of the planets in our Solar System are elliptical, not circular (or epicyclic), as had previously been believed, and that the Dominicus is not located at the center of the orbits, but rather at i focus.^[6] Second, he found that the orbital speed of each planet is not constant, as had previously been idea, merely rather that the speed depends on the planet's distance from the Sun. Third, Kepler institute a universal relationship betwixt the orbital backdrop of all the planets orbiting the Sun. For the planets, the cubes of their distances from the Sun are proportional to the squares of their orbital periods. Jupiter and Venus, for example, are respectively about v.2 and 0.723 AU distant from the Sun, their orbital periods respectively near 11.86 and 0.615 years. The proportionality is seen past the fact that the ratio for Jupiter, 5.2³/11.86ⁱⁱ, is practically equal to that for Venus, 0.723³/0.615², in accord with the human relationship. Idealised orbits meeting these rules are known equally Kepler orbits.

The lines traced out by orbits dominated past the gravity of a central source are conic sections: the shapes of the curves of intersection between a plane and a cone. Parabolic (1) and hyperbolic (3) orbits are escape orbits, whereas elliptical and circular orbits (2) are captive.

This image shows the 4 trajectory categories with the gravitational potential well of the central mass's field of potential free energy shown in black and the tiptop of the kinetic energy of the moving body shown in red extending above that, correlating to changes in speed every bit distance changes co-ordinate to Kepler'southward laws.

Isaac Newton demonstrated that Kepler'southward laws were derivable from his theory of gravitation and that, in general, the orbits of bodies discipline to gravity were conic sections (this assumes that the force of gravity propagates instantaneously). Newton showed that, for a pair of bodies, the orbits' sizes are in changed proportion to their masses, and that those bodies orbit their common center of mass. Where one trunk is much more than massive than the other (as is the case of an artificial satellite orbiting a planet), it is a convenient approximation to take the center of mass as coinciding with the center of the more massive body.

Advances in Newtonian mechanics were then used to explore variations from the simple assumptions backside Kepler orbits, such as the perturbations due to other bodies, or the impact of spheroidal rather than spherical bodies. Lagrange (1736–1813) developed a new arroyo to Newtonian mechanics emphasizing energy more than force, and fabricated progress on the three body problem, discovering the Lagrangian points. In a dramatic vindication of classical mechanics, in 1846 Urbain Le Verrier was able to predict the position of Neptune based on unexplained perturbations in the orbit of Uranus.

Albert Einstein (1879-1955) in his 1916 paper The Foundation of the General Theory of Relativity explained that gravity was due to curvature of space-fourth dimension and removed Newton's assumption that changes propagate instantaneously. This led astronomers to recognize that Newtonian mechanics did not provide the highest accuracy in agreement orbits. In relativity theory, orbits follow geodesic trajectories which are commonly approximated very well by the Newtonian predictions (except where at that place are very potent gravity fields and very high speeds) just the differences are measurable. Essentially all the experimental prove that can distinguish betwixt the theories agrees with relativity theory to within experimental measurement accuracy. The original vindication of full general relativity is that it was able to account for the remaining unexplained amount in precession of Mercury's perihelion first noted by Le Verrier. Still, Newton'south solution is still used for most short term purposes since it is significantly easier to use and sufficiently accurate.

Planetary orbits [edit]

Within a planetary system, planets, dwarf planets, asteroids and other modest planets, comets, and space debris orbit the system's barycenter in elliptical orbits. A comet in a parabolic or hyperbolic orbit near a barycenter is not gravitationally bound to the star and therefore is non considered part of the star'south planetary organisation. Bodies that are gravitationally leap to ane of the planets in a planetary system, either natural or artificial satellites, follow orbits near a barycenter near or within that planet.

Owing to mutual gravitational perturbations, the eccentricities of the planetary orbits vary over time. Mercury, the smallest planet in the Solar System, has the most eccentric orbit. At the present epoch, Mars has the adjacent largest eccentricity while the smallest orbital eccentricities are seen with Venus and Neptune.

As two objects orbit each other, the periapsis is that point at which the two objects are closest to each other and the apoapsis is that point at which they are the farthest. (More specific terms are used for specific bodies. For case, perigee and apogee are the everyman and highest parts of an orbit around Earth, while perihelion and aphelion are the closest and farthest points of an orbit around the Sun.)

In the case of planets orbiting a star, the mass of the star and all its satellites are calculated to be at a unmarried indicate called the barycenter. The paths of all the star'due south satellites are elliptical orbits about that barycenter. Each satellite in that system volition have its ain elliptical orbit with the barycenter at one focal point of that ellipse. At any betoken along its orbit, whatsoever satellite will accept a sure value of kinetic and potential free energy with respect to the barycenter, and that energy is a constant value at every point along its orbit. As a result, as a planet approaches periapsis, the planet will increment in speed as its potential energy decreases; as a planet approaches apoapsis, its velocity will decrease as its potential energy increases.

Understanding orbits [edit]

There are a few common ways of understanding orbits:

A force, such as gravity, pulls an object into a curved path as it attempts to fly off in a straight line.
As the object is pulled toward the massive body, it falls toward that body. However, if it has plenty tangential velocity it will non autumn into the trunk but will instead go on to follow the curved trajectory caused by that trunk indefinitely. The object is then said to be orbiting the torso.

As an illustration of an orbit around a planet, the Newton'due south missive model may evidence useful (see image below). This is a 'thought experiment', in which a cannon on meridian of a alpine mount is able to burn a cannonball horizontally at any called cage speed. The effects of air friction on the cannonball are ignored (or perhaps the mount is high enough that the cannon is above the Earth'south atmosphere, which is the same thing).^[7]

Conic sections describe the possible orbits (yellow) of pocket-sized objects around the Earth. A project of these orbits onto the gravitational potential (bluish) of the Globe makes information technology possible to decide the orbital free energy at each point in space.

If the cannon fires its brawl with a low initial speed, the trajectory of the ball curves downward and hits the basis (A). Equally the firing speed is increased, the cannonball hits the ground farther (B) away from the cannon, considering while the ball is still falling towards the ground, the ground is increasingly curving away from it (see beginning bespeak, above). All these motions are actually "orbits" in a technical sense—they are describing a portion of an elliptical path around the middle of gravity—just the orbits are interrupted by striking the Earth.

If the cannonball is fired with sufficient speed, the ground curves abroad from the brawl at least equally much as the ball falls—so the ball never strikes the footing. It is at present in what could be called a non-interrupted or circumnavigating, orbit. For any specific combination of height above the center of gravity and mass of the planet, in that location is one specific firing speed (unaffected past the mass of the ball, which is assumed to be very small-scale relative to the Earth's mass) that produces a circular orbit, as shown in (C).

As the firing speed is increased beyond this, non-interrupted elliptic orbits are produced; ane is shown in (D). If the initial firing is above the surface of the Earth every bit shown, there will also exist not-interrupted elliptical orbits at slower firing speed; these will come closest to the Earth at the point half an orbit beyond, and directly contrary the firing point, below the round orbit.

At a specific horizontal firing speed called escape velocity, dependent on the mass of the planet and the distance of the object from the barycenter, an open orbit (E) is achieved that has a parabolic path. At even greater speeds the object will follow a range of hyperbolic trajectories. In a practical sense, both of these trajectory types mean the object is "breaking free" of the planet's gravity, and "going off into space" never to render.

The velocity human relationship of two moving objects with mass can thus be considered in four practical classes, with subtypes:

No orbit

Suborbital trajectories

Range of interrupted elliptical paths

Orbital trajectories (or simply, orbits)

Range of elliptical paths with closest betoken opposite firing point
Circular path
Range of elliptical paths with closest point at firing point

Open up (or escape) trajectories

Parabolic paths
Hyperbolic paths

It is worth noting that orbital rockets are launched vertically at first to lift the rocket to a higher place the temper (which causes frictional drag), and then slowly pitch over and finish firing the rocket engine parallel to the atmosphere to achieve orbit speed.

Once in orbit, their speed keeps them in orbit to a higher place the atmosphere. If e.g., an elliptical orbit dips into dense air, the object will lose speed and re-enter (i.e. fall). Occasionally a infinite craft will intentionally intercept the temper, in an act commonly referred to as an aerobraking maneuver.

Newton'south laws of motion [edit]

Newton'southward constabulary of gravitation and laws of motion for two-body problems [edit]

In virtually situations, relativistic effects can be neglected, and Newton's laws give a sufficiently accurate description of motion. The acceleration of a body is equal to the sum of the forces acting on it, divided by its mass, and the gravitational force acting on a body is proportional to the product of the masses of the two attracting bodies and decreases inversely with the foursquare of the distance between them. To this Newtonian approximation, for a system of 2-signal masses or spherical bodies, only influenced by their common gravitation (called a two-trunk problem), their trajectories can be exactly calculated. If the heavier body is much more massive than the smaller, every bit in the case of a satellite or small-scale moon orbiting a planet or for the World orbiting the Sun, it is authentic enough and convenient to describe the movement in terms of a coordinate system that is centered on the heavier body, and we say that the lighter body is in orbit effectually the heavier. For the case where the masses of 2 bodies are comparable, an exact Newtonian solution is still sufficient and can be had by placing the coordinate system at the center of the mass of the arrangement.

Defining gravitational potential free energy [edit]

Free energy is associated with gravitational fields. A stationary body far from another can do external work if it is pulled towards it, and therefore has gravitational potential energy. Since work is required to split two bodies against the pull of gravity, their gravitational potential energy increases as they are separated, and decreases as they arroyo i some other. For point masses, the gravitational energy decreases to zero as they approach zero separation. It is convenient and conventional to assign the potential free energy as having zero value when they are an space altitude autonomously, and hence it has a negative value (since it decreases from zero) for smaller finite distances.

Orbital energies and orbit shapes [edit]

When only two gravitational bodies interact, their orbits follow a conic section. The orbit can be open (implying the object never returns) or closed (returning). Which it is depends on the full free energy (kinetic + potential energy) of the system. In the instance of an open orbit, the speed at whatsoever position of the orbit is at least the escape velocity for that position, in the case of a closed orbit, the speed is always less than the escape velocity. Since the kinetic energy is never negative if the mutual convention is adopted of taking the potential energy as zero at infinite separation, the bound orbits will have negative total energy, the parabolic trajectories nada total energy, and hyperbolic orbits positive full energy.

An open orbit volition accept a parabolic shape if it has the velocity of exactly the escape velocity at that bespeak in its trajectory, and it will have the shape of a hyperbola when its velocity is greater than the escape velocity. When bodies with escape velocity or greater approach each other, they volition briefly curve around each other at the time of their closest approach, and and then separate, forever.

All airtight orbits have the shape of an ellipse. A round orbit is a special case, wherein the foci of the ellipse coincide. The point where the orbiting torso is closest to Earth is chosen the perigee, and is chosen the periapsis (less properly, "perifocus" or "pericentron") when the orbit is nigh a body other than Earth. The betoken where the satellite is farthest from Earth is called the apogee, apoapsis, or sometimes apifocus or apocentron. A line drawn from periapsis to apoapsis is the line-of-apsides. This is the major centrality of the ellipse, the line through its longest part.

Kepler's laws [edit]

Log-log plot of period T vs semi-major centrality a (average of aphelion and perihelion) of some Solar Organisation orbits (crosses denoting Kepler'south values) showing that a³/T² is constant (green line)

Bodies following closed orbits echo their paths with a certain time called the period. This motion is described by the empirical laws of Kepler, which tin be mathematically derived from Newton'southward laws. These can be formulated every bit follows:

The orbit of a planet around the Sun is an ellipse, with the Sun in one of the focal points of that ellipse. [This focal betoken is really the barycenter of the Sun-planet system; for simplicity, this explanation assumes the Sun's mass is infinitely larger than that planet's.] The planet'due south orbit lies in a plane, called the orbital aeroplane. The betoken on the orbit closest to the attracting body is the periapsis. The point farthest from the attracting torso is called the apoapsis. There are also specific terms for orbits well-nigh detail bodies; things orbiting the Sun take a perihelion and aphelion, things orbiting the Globe have a perigee and apogee, and things orbiting the Moon take a perilune and apolune (or periselene and aposelene respectively). An orbit around any star, not just the Sun, has a periastron and an apastron.
As the planet moves in its orbit, the line from the Lord's day to the planet sweeps a constant area of the orbital plane for a given menstruation of time, regardless of which part of its orbit the planet traces during that period of time. This means that the planet moves faster nigh its perihelion than near its aphelion, considering at the smaller distance it needs to trace a greater arc to cover the same area. This constabulary is normally stated every bit "equal areas in equal fourth dimension."
For a given orbit, the ratio of the cube of its semi-major centrality to the square of its period is constant.

Limitations of Newton's police force of gravitation [edit]

Notation that while bound orbits of a point mass or a spherical torso with a Newtonian gravitational field are airtight ellipses, which repeat the same path exactly and indefinitely, whatsoever non-spherical or not-Newtonian furnishings (such as caused by the slight oblateness of the Earth, or by relativistic furnishings, thereby changing the gravitational field's behavior with distance) will cause the orbit's shape to depart from the closed ellipses characteristic of Newtonian two-torso motility. The two-trunk solutions were published by Newton in Principia in 1687. In 1912, Karl Fritiof Sundman developed a converging space series that solves the three-body problem; however, it converges also slowly to be of much utilise. Except for special cases like the Lagrangian points, no method is known to solve the equations of motion for a organization with iv or more than bodies.

Approaches to many-torso issues [edit]

Rather than an exact airtight course solution, orbits with many bodies can be approximated with arbitrarily high accuracy. These approximations take ii forms:

Ane form takes the pure elliptic motion every bit a basis and adds perturbation terms to account for the gravitational influence of multiple bodies. This is convenient for calculating the positions of astronomical bodies. The equations of motion of the moons, planets, and other bodies are known with swell accuracy, and are used to generate tables for celestial navigation. Still, in that location are secular phenomena that take to be dealt with by post-Newtonian methods.

The differential equation class is used for scientific or mission-planning purposes. According to Newton's laws, the sum of all the forces acting on a body will equal the mass of the body times its acceleration (F = ma). Therefore accelerations tin be expressed in terms of positions. The perturbation terms are much easier to depict in this form. Predicting subsequent positions and velocities from initial values of position and velocity corresponds to solving an initial value problem. Numerical methods calculate the positions and velocities of the objects a short time in the future, and then repeat the adding ad nauseam. Withal, tiny arithmetic errors from the limited accuracy of a computer's math are cumulative, which limits the accuracy of this approach.

Differential simulations with large numbers of objects perform the calculations in a hierarchical pairwise fashion between centers of mass. Using this scheme, galaxies, star clusters and other big assemblages of objects have been fake.^{[ citation needed ]}

Newtonian assay of orbital motion [edit]

The post-obit derivation applies to such an elliptical orbit. Nosotros start only with the Newtonian police of gravitation stating that the gravitational dispatch towards the fundamental body is related to the inverse of the square of the distance between them, namely

F_{2}=-{\frac {Gm_{1}m_{ii}}{r^{two}}}

where F _two is the force acting on the mass m _ii caused by the gravitational attraction mass grand ₁ has for m ₂, Chiliad is the universal gravitational constant, and r is the distance between the two masses centers.

From Newton's 2nd Constabulary, the summation of the forces acting on thousand ₂ related to that body'southward dispatch:

F_{two}=m_{ii}A_{ii}

where A _ii is the acceleration of m _ii caused by the force of gravitational attraction F _ii of one thousand ₁ acting on one thousand _two.

Combining Eq. 1 and 2:

-{\frac {Gm_{1}m_{two}}{r^{2}}}=m_{2}A_{two}

Solving for the acceleration, A ₂:

A_{ii}={\frac {F_{two}}{m_{two}}}=-{\frac {1}{m_{2}}}{\frac {Gm_{1}m_{2}}{r^{2}}}=-{\frac {\mu }{r^{two}}}

where $\mu \,$ is the standard gravitational parameter, in this case $Gm_{1}$ . It is understood that the system beingness described is k ₂, hence the subscripts can be dropped.

Nosotros assume that the central trunk is massive plenty that it can be considered to be stationary and nosotros ignore the more subtle effects of general relativity.

When a pendulum or an object attached to a spring swings in an ellipse, the inward acceleration/forcefulness is proportional to the distance $A=F/1000=-kr.$ Due to the way vectors add, the component of the force in the ${\chapeau {\mathbf {10} }}$ or in the ${\hat {\mathbf {y} }}$ directions are besides proportionate to the respective components of the distances, $r''_{x}=A_{x}=-kr_{ten}$ . Hence, the entire analysis can be washed separately in these dimensions. This results in the harmonic parabolic equations $x=A\cos(t)$ and $y=B\sin(t)$ of the ellipse. In contrast, with the decreasing relationship $A=\mu /r^{2}$ , the dimensions cannot be separated.^{[ citation needed ]}

The location of the orbiting object at the current time $t$ is located in the plane using vector calculus in polar coordinates both with the standard Euclidean basis and with the polar basis with the origin coinciding with the centre of forcefulness. Let $r$ be the distance betwixt the object and the center and $\theta$ be the bending information technology has rotated. Let ${\hat {\mathbf {ten} }}$ and ${\hat {\mathbf {y} }}$ exist the standard Euclidean bases and let ${\hat {\mathbf {r} }}=\cos(\theta ){\hat {\mathbf {x} }}+\sin(\theta ){\hat {\mathbf {y} }}$ and ${\hat {\boldsymbol {\theta }}}=-\sin(\theta ){\chapeau {\mathbf {x} }}+\cos(\theta ){\hat {\mathbf {y} }}$ exist the radial and transverse polar footing with the start being the unit of measurement vector pointing from the cardinal torso to the current location of the orbiting object and the 2d beingness the orthogonal unit vector pointing in the direction that the orbiting object would travel if orbiting in a counter clockwise circle. So the vector to the orbiting object is

{\hat {\mathbf {O} }}=r\cos(\theta ){\hat {\mathbf {10} }}+r\sin(\theta ){\hat {\mathbf {y} }}=r{\hat {\mathbf {r} }}

We employ ${\dot {r}}$ and ${\dot {\theta }}$ to denote the standard derivatives of how this distance and angle alter over time. We take the derivative of a vector to run across how information technology changes over time past subtracting its location at fourth dimension $t$ from that at fourth dimension $t+\delta t$ and dividing by $\delta t$ . The event is also a vector. Because our ground vector ${\chapeau {\mathbf {r} }}$ moves every bit the object orbits, nosotros start by differentiating it. From time $t$ to $t+\delta t$ , the vector ${\hat {\mathbf {r} }}$ keeps its beginning at the origin and rotates from angle $\theta$ to $\theta +{\dot {\theta }}\ \delta t$ which moves its head a altitude ${\dot {\theta }}\ \delta t$ in the perpendicular management ${\hat {\boldsymbol {\theta }}}$ giving a derivative of ${\dot {\theta }}{\hat {\boldsymbol {\theta }}}$ .

{\begin{aligned}{\hat {\mathbf {r} }}&=\cos(\theta ){\lid {\mathbf {ten} }}+\sin(\theta ){\lid {\mathbf {y} }}\\{\frac {\delta {\hat {\mathbf {r} }}}{\delta t}}={\dot {\mathbf {r} }}&=-\sin(\theta ){\dot {\theta }}{\hat {\mathbf {x} }}+\cos(\theta ){\dot {\theta }}{\lid {\mathbf {y} }}={\dot {\theta }}{\hat {\boldsymbol {\theta }}}\\{\hat {\boldsymbol {\theta }}}&=-\sin(\theta ){\hat {\mathbf {x} }}+\cos(\theta ){\hat {\mathbf {y} }}\\{\frac {\delta {\hat {\boldsymbol {\theta }}}}{\delta t}}={\dot {\boldsymbol {\theta }}}&=-\cos(\theta ){\dot {\theta }}{\lid {\mathbf {x} }}-\sin(\theta ){\dot {\theta }}{\lid {\mathbf {y} }}=-{\dot {\theta }}{\lid {\mathbf {r} }}\finish{aligned}}

We can now find the velocity and acceleration of our orbiting object.

{\begin{aligned}{\hat {\mathbf {O} }}&=r{\chapeau {\mathbf {r} }}\\{\dot {\mathbf {O} }}&={\frac {\delta r}{\delta t}}{\hat {\mathbf {r} }}+r{\frac {\delta {\hat {\mathbf {r} }}}{\delta t}}={\dot {r}}{\hat {\mathbf {r} }}+r\left[{\dot {\theta }}{\hat {\boldsymbol {\theta }}}\right]\\{\ddot {\mathbf {O} }}&=\left[{\ddot {r}}{\chapeau {\mathbf {r} }}+{\dot {r}}{\dot {\theta }}{\lid {\boldsymbol {\theta }}}\right]+\left[{\dot {r}}{\dot {\theta }}{\hat {\boldsymbol {\theta }}}+r{\ddot {\theta }}{\hat {\boldsymbol {\theta }}}-r{\dot {\theta }}^{2}{\hat {\mathbf {r} }}\right]\\&=\left[{\ddot {r}}-r{\dot {\theta }}^{2}\right]{\hat {\mathbf {r} }}+\left[r{\ddot {\theta }}+ii{\dot {r}}{\dot {\theta }}\right]{\hat {\boldsymbol {\theta }}}\end{aligned}}

The coefficients of ${\chapeau {\mathbf {r} }}$ and ${\hat {\boldsymbol {\theta }}}$ give the accelerations in the radial and transverse directions. Every bit said, Newton gives this first due to gravity is $-\mu /r^{2}$ and the second is zip.

${\ddot {r}}-r{\dot {\theta }}^{2}=-{\frac {\mu }{r^{two}}}$

(one)

$r{\ddot {\theta }}+two{\dot {r}}{\dot {\theta }}=0$

(2)

Equation (2) can be rearranged using integration past parts.

r{\ddot {\theta }}+two{\dot {r}}{\dot {\theta }}={\frac {1}{r}}{\frac {d}{dt}}\left(r^{2}{\dot {\theta }}\correct)=0

Nosotros tin multiply through past $r$ because it is not zip unless the orbiting object crashes. Then having the derivative exist nil gives that the function is a abiding.

$r^{2}{\dot {\theta }}=h$

(iii)

which is actually the theoretical proof of Kepler's 2d law (A line joining a planet and the Sun sweeps out equal areas during equal intervals of fourth dimension). The abiding of integration, h, is the athwart momentum per unit of measurement mass.

In order to get an equation for the orbit from equation (i), we need to eliminate fourth dimension.^[eight] (Encounter too Binet equation.) In polar coordinates, this would limited the distance $r$ of the orbiting object from the centre as a office of its angle $\theta$ . However, it is easier to introduce the auxiliary variable $u=1/r$ and to express $u$ as a function of $\theta$ . Derivatives of $r$ with respect to time may exist rewritten as derivatives of $u$ with respect to angle.

u={1 \over r}

{\dot {\theta }}={\frac {h}{r^{two}}}=hu^{two}

(reworking (three))

{\brainstorm{aligned}{\frac {\delta u}{\delta \theta }}&={\frac {\delta }{\delta t}}\left({\frac {one}{r}}\right){\frac {\delta t}{\delta \theta }}=-{\frac {\dot {r}}{r^{two}{\dot {\theta }}}}=-{\frac {\dot {r}}{h}}\\{\frac {\delta ^{2}u}{\delta \theta ^{2}}}&=-{\frac {1}{h}}{\frac {\delta {\dot {r}}}{\delta t}}{\frac {\delta t}{\delta \theta }}=-{\frac {\ddot {r}}{h{\dot {\theta }}}}=-{\frac {\ddot {r}}{h^{2}u^{2}}}\ \ \ {\text{ or }}\ \ \ {\ddot {r}}=-h^{ii}u^{two}{\frac {\delta ^{2}u}{\delta \theta ^{2}}}\end{aligned}}

Plugging these into (1) gives

{\begin{aligned}{\ddot {r}}-r{\dot {\theta }}^{2}&=-{\frac {\mu }{r^{2}}}\\-h^{ii}u^{2}{\frac {\delta ^{two}u}{\delta \theta ^{ii}}}-{\frac {1}{u}}\left(hu^{2}\right)^{ii}&=-\mu u^{ii}\cease{aligned}}

${\frac {\delta ^{two}u}{\delta \theta ^{2}}}+u={\frac {\mu }{h^{2}}}$

(4)

So for the gravitational force – or, more generally, for any inverse square strength law – the correct hand side of the equation becomes a constant and the equation is seen to exist the harmonic equation (up to a shift of origin of the dependent variable). The solution is:

u(\theta )={\frac {\mu }{h^{2}}}-A\cos(\theta -\theta _{0})

where A and θ ₀ are arbitrary constants. This resulting equation of the orbit of the object is that of an ellipse in Polar class relative to ane of the focal points. This is put into a more standard class by letting $e\equiv h^{ii}A/\mu$ be the eccentricity, letting $a\equiv h^{2}/\mu \left(1-due east^{2}\right)$ be the semi-major axis. Finally, letting $\theta _{0}\equiv 0$ so the long axis of the ellipse is forth the positive x coordinate.

r(\theta )={\frac {a\left(one-e^{ii}\right)}{1+e\cos \theta }}

When the two-body organization is under the influence of torque, the athwart momentum h is not a constant. After the following adding:

{\begin{aligned}{\frac {\delta r}{\delta \theta }}&=-{\frac {1}{u^{2}}}{\frac {\delta u}{\delta \theta }}=-{\frac {h}{1000}}{\frac {\delta u}{\delta \theta }}\\{\frac {\delta ^{ii}r}{\delta \theta ^{two}}}&=-{\frac {h^{2}u^{2}}{m^{2}}}{\frac {\delta ^{2}u}{\delta \theta ^{2}}}-{\frac {hu^{2}}{m^{2}}}{\frac {\delta h}{\delta \theta }}{\frac {\delta u}{\delta \theta }}\\\left({\frac {\delta \theta }{\delta t}}\right)^{two}r&={\frac {h^{2}u^{iii}}{grand^{2}}}\terminate{aligned}}

we volition get the Sturm-Liouville equation of ii-body system.^[9]

${\frac {\delta }{\delta \theta }}\left(h{\frac {\delta u}{\delta \theta }}\right)+hu={\frac {\mu }{h}}$

(5)

Relativistic orbital movement [edit]

The above classical (Newtonian) analysis of orbital mechanics assumes that the more subtle effects of general relativity, such as frame dragging and gravitational time dilation are negligible. Relativistic furnishings cease to be negligible when near very massive bodies (as with the precession of Mercury's orbit about the Sun), or when extreme precision is needed (as with calculations of the orbital elements and time betoken references for GPS satellites.^[10]).

Orbital planes [edit]

The assay so far has been 2 dimensional; it turns out that an unperturbed orbit is two-dimensional in a plane stock-still in space, and thus the extension to three dimensions requires but rotating the two-dimensional plane into the required bending relative to the poles of the planetary trunk involved.

The rotation to do this in 3 dimensions requires three numbers to uniquely determine; traditionally these are expressed every bit three angles.

Orbital period [edit]

The orbital menstruum is simply how long an orbiting trunk takes to complete one orbit.

Specifying orbits [edit]

Half-dozen parameters are required to specify a Keplerian orbit most a body. For example, the 3 numbers that specify the body'due south initial position, and the three values that specify its velocity will define a unique orbit that can be calculated forrard (or backwards) in time. However, traditionally the parameters used are slightly different.

The traditionally used set of orbital elements is chosen the set up of Keplerian elements, later Johannes Kepler and his laws. The Keplerian elements are six:

Inclination (i)
Longitude of the ascending node (Ω)
Argument of periapsis (ω)
Eccentricity (east)
Semimajor axis (a)
Mean anomaly at epoch (1000 ₀).

In principle, once the orbital elements are known for a body, its position can be calculated forward and backward indefinitely in time. Nonetheless, in exercise, orbits are affected or perturbed, by other forces than simple gravity from an causeless bespeak source (see the next department), and thus the orbital elements change over time.

Orbital perturbations [edit]

An orbital perturbation is when a force or impulse which is much smaller than the overall force or average impulse of the main gravitating torso and which is external to the two orbiting bodies causes an acceleration, which changes the parameters of the orbit over time.

Radial, prograde and transverse perturbations [edit]

A pocket-sized radial impulse given to a body in orbit changes the eccentricity, simply not the orbital period (to first club). A prograde or retrograde impulse (i.e. an impulse applied along the orbital movement) changes both the eccentricity and the orbital period. Notably, a prograde impulse at periapsis raises the distance at apoapsis, and vice versa and a retrograde impulse does the contrary. A transverse impulse (out of the orbital plane) causes rotation of the orbital plane without irresolute the catamenia or eccentricity. In all instances, a closed orbit will still intersect the perturbation point.

Orbital decay [edit]

If an orbit is about a planetary trunk with a pregnant atmosphere, its orbit can decay considering of drag. Particularly at each periapsis, the object experiences atmospheric drag, losing energy. Each time, the orbit grows less eccentric (more circular) considering the object loses kinetic free energy precisely when that free energy is at its maximum. This is similar to the effect of slowing a pendulum at its lowest point; the highest point of the pendulum'southward swing becomes lower. With each successive slowing more than of the orbit's path is affected by the atmosphere and the effect becomes more pronounced. Somewhen, the effect becomes and then great that the maximum kinetic energy is not enough to return the orbit above the limits of the atmospheric drag effect. When this happens the body will rapidly spiral down and intersect the fundamental torso.

The bounds of an atmosphere vary wildly. During a solar maximum, the Earth's atmosphere causes drag up to a hundred kilometres higher than during a solar minimum.

Some satellites with long conductive tethers can also experience orbital decay because of electromagnetic drag from the Globe'due south magnetic field. As the wire cuts the magnetic field it acts as a generator, moving electrons from i terminate to the other. The orbital energy is converted to heat in the wire.

Orbits can exist artificially influenced through the use of rocket engines which alter the kinetic energy of the trunk at some betoken in its path. This is the conversion of chemical or electrical energy to kinetic energy. In this manner changes in the orbit shape or orientation tin exist facilitated.

Another method of artificially influencing an orbit is through the use of solar sails or magnetic sails. These forms of propulsion require no propellant or free energy input other than that of the Sunday, and and so tin be used indefinitely. See statite for one such proposed use.

Orbital disuse can occur due to tidal forces for objects below the synchronous orbit for the body they're orbiting. The gravity of the orbiting object raises tidal bulges in the chief, and since beneath the synchronous orbit, the orbiting object is moving faster than the body's surface the bulges lag a brusk bending behind it. The gravity of the bulges is slightly off of the primary-satellite axis and thus has a component along with the satellite's motion. The near bulge slows the object more than the far bulge speeds information technology up, and equally a result, the orbit decays. Conversely, the gravity of the satellite on the bulges applies torque on the primary and speeds upward its rotation. Artificial satellites are as well small to take an observable tidal consequence on the planets they orbit, but several moons in the Solar Organisation are undergoing orbital disuse by this mechanism. Mars' innermost moon Phobos is a prime example and is expected to either impact Mars' surface or break up into a ring inside 50 million years.

Orbits can decay via the emission of gravitational waves. This mechanism is extremely weak for most stellar objects, but becoming significant in cases where there is a combination of extreme mass and extreme acceleration, such equally with black holes or neutron stars that are orbiting each other closely.

Oblateness [edit]

The standard analysis of orbiting bodies assumes that all bodies consist of uniform spheres, or more generally, concentric shells each of uniform density. It tin can exist shown that such bodies are gravitationally equivalent to bespeak sources.

However, in the real world, many bodies rotate, and this introduces oblateness and distorts the gravity field, and gives a quadrupole moment to the gravitational field which is meaning at distances comparable to the radius of the body. In the general instance, the gravitational potential of a rotating trunk such as, due east.k., a planet is normally expanded in multipoles accounting for the departures of it from spherical symmetry. From the point of view of satellite dynamics, of particular relevance are the so-chosen even zonal harmonic coefficients, or fifty-fifty zonals, since they induce secular orbital perturbations which are cumulative over time spans longer than the orbital period.^[11] ^[12] ^[xiii] They exercise depend on the orientation of the body's symmetry axis in the infinite, affecting, in general, the whole orbit, with the exception of the semimajor axis.

Multiple gravitating bodies [edit]

The effects of other gravitating bodies tin exist meaning. For example, the orbit of the Moon cannot exist accurately described without assuasive for the activeness of the Sun'southward gravity as well as the Earth's. One estimate result is that bodies volition ordinarily have reasonably stable orbits effectually a heavier planet or moon, in spite of these perturbations, provided they are orbiting well within the heavier body'southward Hill sphere.

When there are more than than ii gravitating bodies it is referred to as an n-torso problem. Nigh n-body bug have no closed grade solution, although some special cases accept been formulated.

Light radiations and stellar wind [edit]

For smaller bodies specially, lite and stellar wind can cause pregnant perturbations to the mental attitude and management of motion of the body, and over time tin exist pregnant. Of the planetary bodies, the motion of asteroids is particularly affected over large periods when the asteroids are rotating relative to the Sun.

Strange orbits [edit]

Mathematicians have discovered that it is possible in principle to have multiple bodies in non-elliptical orbits that repeat periodically, although nigh such orbits are not stable regarding small perturbations in mass, position, or velocity. However, some special stable cases have been identified, including a planar figure-viii orbit occupied past iii moving bodies.^[14] Further studies have discovered that nonplanar orbits are also possible, including i involving 12 masses moving in 4 roughly circular, interlocking orbits topologically equivalent to the edges of a cuboctahedron.^[fifteen]

Finding such orbits naturally occurring in the universe is idea to exist extremely unlikely, because of the improbability of the required conditions occurring by run a risk.^[15]

Astrodynamics [edit]

Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the applied problems apropos the motion of rockets and other spacecraft. The movement of these objects is ordinarily calculated from Newton's laws of motion and Newton's constabulary of universal gravitation. It is a core discipline inside infinite mission design and control. Celestial mechanics treats more broadly the orbital dynamics of systems under the influence of gravity, including spacecraft and natural astronomical bodies such as star systems, planets, moons, and comets. Orbital mechanics focuses on spacecraft trajectories, including orbital maneuvers, orbit plane changes, and interplanetary transfers, and is used by mission planners to predict the results of propulsive maneuvers. General relativity is a more exact theory than Newton's laws for calculating orbits, and is sometimes necessary for greater accurateness or in high-gravity situations (such as orbits close to the Lord's day).

Earth orbits [edit]

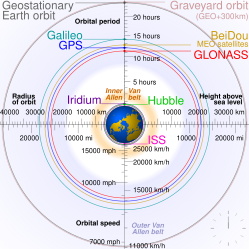
Low Earth orbit (LEO): Geocentric orbits with altitudes up to 2,000 km (0–1,240 miles).^[16]
Medium Earth orbit (MEO): Geocentric orbits ranging in altitude from 2,000 km (1,240 miles) to just below geosynchronous orbit at 35,786 kilometers (22,236 mi). Also known every bit an intermediate circular orbit. These are "most commonly at 20,200 kilometers (12,600 mi), or 20,650 kilometers (12,830 mi), with an orbital period of 12 hours."^[17]
Both geosynchronous orbit (GSO) and geostationary orbit (GEO) are orbits effectually Globe matching Earth's sidereal rotation menstruation. All geosynchronous and geostationary orbits have a semi-major centrality of 42,164 km (26,199 mi).^[eighteen] All geostationary orbits are also geosynchronous, merely non all geosynchronous orbits are geostationary. A geostationary orbit stays exactly to a higher place the equator, whereas a geosynchronous orbit may swing north and south to comprehend more than of the World'due south surface. Both complete one full orbit of Earth per sidereal twenty-four hour period (relative to the stars, not the Sun).
High Earth orbit: Geocentric orbits above the altitude of geosynchronous orbit 35,786 km (22,240 miles).^[17]

Scaling in gravity [edit]

The gravitational constant K has been calculated every bit:

(vi.6742 ± 0.001) × 10⁻¹¹ (kg/m³)^−anes⁻².

Thus the constant has dimension density⁻¹ time⁻ⁱⁱ. This corresponds to the following properties.

Scaling of distances (including sizes of bodies, while keeping the densities the same) gives similar orbits without scaling the fourth dimension: if for example distances are halved, masses are divided past eight, gravitational forces past xvi and gravitational accelerations by 2. Hence velocities are halved and orbital periods and other travel times related to gravity remain the same. For example, when an object is dropped from a tower, the time it takes to fall to the basis remains the aforementioned with a scale model of the tower on a calibration model of the World.

Scaling of distances while keeping the masses the aforementioned (in the case of betoken masses, or by adjusting the densities) gives similar orbits; if distances are multiplied by 4, gravitational forces and accelerations are divided by sixteen, velocities are halved and orbital periods are multiplied past viii.

When all densities are multiplied by 4, orbits are the same; gravitational forces are multiplied by xvi and accelerations past four, velocities are doubled and orbital periods are halved.

When all densities are multiplied by 4, and all sizes are halved, orbits are similar; masses are divided by ii, gravitational forces are the aforementioned, gravitational accelerations are doubled. Hence velocities are the same and orbital periods are halved.

In all these cases of scaling. if densities are multiplied by 4, times are halved; if velocities are doubled, forces are multiplied by xvi.

These properties are illustrated in the formula (derived from the formula for the orbital flow)

GT^{ii}\rho =3\pi \left({\frac {a}{r}}\correct)^{3},

for an elliptical orbit with semi-major axis a, of a small torso around a spherical torso with radius r and average density ρ, where T is the orbital menstruation. See also Kepler's 3rd Law.

Patents [edit]

The awarding of sure orbits or orbital maneuvers to specific useful purposes have been the subject of patents.^[19]

Tidal locking [edit]

Some bodies are tidally locked with other bodies, meaning that one side of the celestial body is permanently facing its host object. This is the case for World-Moon and Pluto-Charon system.

Come across also [edit]

Ephemeris is a compilation of positions of naturally occurring astronomical objects as well as bogus satellites in the heaven at a given fourth dimension or times.
Complimentary migrate
Klemperer rosette
Listing of orbits
Molniya orbit
Orbit determination
Orbital spaceflight
Perifocal coordinate system
Polar Orbits
Radial trajectory
Rosetta (orbit)
VSOP (planets)

Notes [edit]

^ Orbital periods and speeds are calculated using the relations 4 $π$ ⁱⁱ R ³ =T ⁱⁱ GM and 5 ^two R =GM, where R = radius of orbit in metres, T = orbital menses in seconds, V = orbital speed in chiliad/s, G = gravitational abiding ≈ 6.673×x^−eleven Nm²/kgⁱⁱ, M = mass of Earth ≈ v.98×ten²⁴ kg.
^ Approximately 8.6 times when the Moon is nearest (363,104 km ÷ 42,164 km) to 9.6 times when the Moon is farthest (405,696 km ÷ 42,164 km).

References [edit]

^ "orbit (astronomy) – Britannica Online Encyclopedia". Archived from the original on 5 May 2015. Retrieved 28 July 2008.
^ "The Space Place :: What's a Barycenter". Archived from the original on 29 January 2013. Retrieved 26 November 2012.
^ Kuhn, The Copernican Revolution, pp. 238, 246–252
^ Encyclopædia Britannica, 1968, vol. ii, p. 645
^ Thousand Caspar, Kepler (1959, Abelard-Schuman), at pp.131–140; A Koyré, The Astronomical Revolution: Copernicus, Kepler, Borelli (1973, Methuen), pp. 277–279
^ Jones, Andrew. "Kepler's Laws of Planetary Movement". nearly.com. Archived from the original on 18 Nov 2016. Retrieved 1 June 2008.
^ See pages 6 to 8 in Newton'southward "Treatise of the System of the World" Archived 30 December 2016 at the Wayback Motorcar (written 1685, translated into English 1728, see Newton's 'Principia' – A preliminary version), for the original version of this 'cannonball' thought-experiment.
^ Fitzpatrick, Richard (two February 2006). "Planetary orbits". Classical Mechanics – an introductory course. The University of Texas at Austin. Archived from the original on 3 March 2001.
^ Luo, Siwei (22 June 2020). "The Sturm-Liouville problem of two-trunk organisation". Periodical of Physics Communications. iv (half-dozen): 061001. Bibcode:2020JPhCo...4f1001L. doi:10.1088/2399-6528/ab9c30.
^ Pogge, Richard W.; "Real-World Relativity: The GPS Navigation System" Archived xiv Nov 2015 at the Wayback Car. Retrieved 25 January 2008.
^ Iorio, L. (2011). "Perturbed stellar motions around the rotating black hole in Sgr A* for a generic orientation of its spin axis". Concrete Review D. 84 (12): 124001. arXiv:1107.2916. Bibcode:2011PhRvD..84l4001I. doi:x.1103/PhysRevD.84.124001. S2CID 118305813.
^ Renzetti, G. (2013). "Satellite Orbital Precessions Caused by the Octupolar Mass Moment of a Not-Spherical Torso Arbitrarily Oriented in Space". Journal of Astrophysics and Astronomy. 34 (four): 341–348. Bibcode:2013JApA...34..341R. doi:10.1007/s12036-013-9186-4. S2CID 120030309.
^ Renzetti, One thousand. (2014). "Satellite orbital precessions caused past the kickoff odd zonal J3 multipole of a not-spherical trunk arbitrarily oriented in space". Astrophysics and Space Science. 352 (2): 493–496. Bibcode:2014Ap&SS.352..493R. doi:x.1007/s10509-014-1915-x. S2CID 119537102.
^ Chenciner, Alain; Montgomery, Richard (31 October 2000). "A remarkable periodic solution of the three-trunk trouble in the case of equal masses". arXiv:math/0011268.
^ ^a ^b Peterson, Ivars (23 September 2013). "Foreign Orbits". Science News. Archived from the original on 22 November 2015. Retrieved 21 July 2017.
^ "NASA Safety Standard 1740.14, Guidelines and Assessment Procedures for Limiting Orbital Debris" (PDF). Role of Rubber and Mission Assurance. 1 August 1995. Archived from the original (PDF) on 15 February 2013. , pages 37-38 (half-dozen-1,6-2); figure 6-1.
^ ^a ^b "Orbit: Definition". Ancillary Description Author's Guide, 2013. National Helmsmanship and Space Administration (NASA) Global Modify Principal Directory. Archived from the original on 11 May 2013. Retrieved 29 April 2013.
^ Vallado, David A. (2007). Fundamentals of Astrodynamics and Applications. Hawthorne, CA: Microcosm Press. p. 31.
^ Ferreira, Becky (19 February 2015). "How Satellite Companies Patent Their Orbits". Motherboard. Vice News. Archived from the original on xviii January 2017. Retrieved 20 September 2018.

Farther reading [edit]

Abell; Morrison & Wolff (1987). Exploration of the Universe (fifth ed.). Saunders College Publishing. ISBN9780030051432.
Linton, Christopher (2004). From Eudoxus to Einstein: A History of Mathematical Astronomy. Cambridge Academy Press. ISBN978-1-139-45379-0.
Frank Swetz; John Fauvel; Bengt Johansson; Victor Katz; Otto Bekken (1995). Learn from the Masters. MAA. ISBN978-0-88385-703-8.
Andrea Milani and Giovanni F. Gronchi. Theory of Orbit Decision (Cambridge Academy Press; 378 pages; 2010). Discusses new algorithms for determining the orbits of both natural and artificial angelic bodies.

External links [edit]

Look up orbit in Wiktionary, the free dictionary.

Wikimedia Commons has media related to Orbits.

CalcTool: Orbital flow of a planet calculator. Has wide choice of units. Requires JavaScript.
Java simulation on orbital motion. Requires Java.
NOAA folio on Climate Forcing Information includes (calculated) data on Globe orbit variations over the final 50 one thousand thousand years and for the coming 20 million years
On-line orbit plotter. Requires JavaScript.
Orbital Mechanics (Rocket and Space Applied science)
Orbital simulations by Varadi, Ghil and Runnegar (2003) provide another, slightly different series for Earth orbit eccentricity, and likewise a series for orbital inclination. Orbits for the other planets were also calculated, past F. Varadi; B. Runnegar; M. Ghil (2003). "Successive Refinements in Long-Term Integrations of Planetary Orbits". The Astrophysical Journal. 592 (1): 620–630. Bibcode:2003ApJ...592..620V. doi:10.1086/375560. , just only the eccentricity data for World and Mercury are bachelor online.
Sympathize orbits using straight manipulation. Requires JavaScript and Macromedia
Merrifield, Michael. "Orbits (including the first manned orbit)". Sixty Symbols. Brady Haran for the Academy of Nottingham.